Cuerpos geométricos

POLIEDROS

Los poliedros son cuerpos geométricos cerrados limitados por polígonos.

Elementos de un poliedro:

Cara: Es cada polígono que limita al poliedro
Vértices: Puntos donde concurren 3 o más caras. Coinciden con los vértices de las caras.
Arista: Son los lados de cada cara (segmentos que unen dos vértices consecutivos)
Diagonal: Es cualquier segmento que une dos vértices no consecutivos.

Poliedros cóncavos y convexos.

Un poliedro cóncavo es el que tiene alguna cara cuyo plano atraviesa la figura, es decir, existe alguna cara que, al prolongarla, corta al poliedro. Se puede decir, de forma intuitiva, que un poliedro cóncavo es aquel que tiene caras que no se pueden apoyar en un plano infinito.

Una característica del poliedro cóncavo es que se si unimos dos puntos del poliedro, la linea de unión no siempre queda dentro.

Un poliedro convexo se caracteriza porque si prolongamos cualquiera de sus caras, esta prolongación no atraviesa a la figura.

Una característica del poliedro convexo, es que cualquier segmento que una dos puntos de éste, siempre se quedará dentro del poliedro.

Fórmula de Euler: 

Cualquier poliedro convexo verifica que: 

Poliedros regulares:

Un poliedro regular es en el que sus caras son polígonos regulares iguales y en cada vértice se une el mismo número de caras.

Sólo existen cinco poliedros regulares que son:

PRISMAS. ÁREA

1º Repasamos el área de figuras planas:

Un prisma es un poliedro que tiene dos caras que son polígonos iguales y paralelos (llamados bases) y el resto de cara son paralelogramos. La altura del prisma es la distancia entre las dos bases.
Clasificación: se puede clasificar según su inclinación y según el polígono que tenga por base.

Los paralepípedos son prismas cuya base es un paralelogramo, y si son rectos y su base es un rectángulo reciben el nombre de ortoedros.

Cálculo del área y volumen de un ortoedro:

Cálculo del área y volumen de un prisma:

El área de cualquier poliedro es la suma de las áreas de los polígonos que la forman, es decir la suma de 2·(área de las bases) mas el área lateral (suma de sus caras laterales).
Ejemplo, como las bases son rectángulos su área es base·altura
Al ser las bases polígonos regulares basta calcular el área de uno de los lados y multiplicar por 4 (nº de lados de la base).
Así el area sería: AREA= area base + 4·(area lado) = 6·2+4·6·10
Si abrimos la figura, el cálculo se simplifica a Area base + (perímetro base) · altura=6·2+(4·6)·10


Cálculo del volumen de un prisma:

Ejemplo:

PIRÁMIDES. ÁREA Y VOLUMEN

Una pirámide es un poliedro que tiene por base un polígono y sus caras laterales son triángulos con un vértice común, llamado vértice de la pirámide. La altura de la pirámide es la distancia de la base a dicho vértice.

TIPOS DE PIRÁMIDE

El área y volumen de una pirámide

SIMETRÍAS EN LOS POLIEDROS

CUERPOS DE REVOLUCIÓN. ÁREA Y VOLUMEN

Un cuerpo de revolución es aquel que se origina al girar una figura plana alrededor de un eje,

En todos los cuerpos de revolución se puede distingur:

Eje de rotación: Recta alrededor de la cual gira la figura plana para generar el cuerpo de reovolución.

Generatriz: es la línea exterior de la figura plana.

VOLUMEN DE CUERPOS GEOMÉTRICOS. LA ESFERA TERRESTRE

El cilindro es un cuerpo geométrico engendrado por el giro de un rectángulo alrededor de uno de sus lados
El cono se obtiene al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.
La esfera es un cuerpo geométrico limitado por una superficie cuyos puntos están todos a igual distancia de uno interior llamado centro.

Ejemplo:

Figuras esféricas:

Zona esférica es la superficie comprendida entre dos planos paralelos, sea este un círculo máximo o no. Su área es igual al producto de una circunferencia máxima por la altura de la zona: (ver figura abajo)

Área zona esférica = 2.¶.R.h

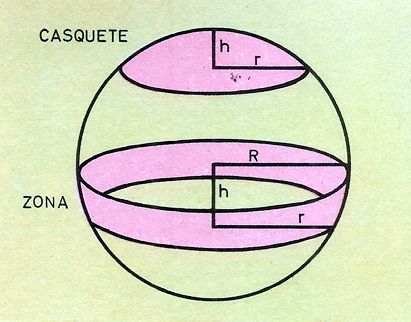
h: es la distancia entre circunferencias del casquete o la altura del casquete
R: radio de la circunferencia máxima

Esta fórmula es igual que la obtenida para el cilindro, es decir, el área de una zona esférica es igual que la de un cilindro de base igual al círculo máximo de la zona, y de altura idéntica a la misma.

Casquete esférico es una zona cuya base superior es un punto. Por tanto, su área vale igual que la de una zona: 2.¶.r.h

r: radio del casquete

Área de la superficie esférica. Es el área total de la esfera es: A= 4.¶.R²

COORDENADAS GEOGRÁFICAS.

El sistema de coordenadas geográficas es un sistema que referencia cualquier punto de la superficie terrestre y que utiliza para ello dos coordenadas angulares, latitud (norte o sur) y longitud (este u oeste), para determinar los ángulos laterales de la superficie terrestre con respecto al centro de la Tierra y alineadas con su eje de rotación.

FORMULAS DE LOS CUERPOS GEOMÉTRICOS: